Correction - Exercice corrigé n°07 - Fonctions linéaires

1ère année secondaire

Fonctions linéaires

Correction - Exercice corrigé n°07

07 - a) \({f}\) est une fonction linéaire donc il existe un réel \({a}\) tel que pour tout réel \({x}\), \({f(x) = ax}\)

Calculons \({a}\) pour \({2f(3)-5f(-2) = {32}}\):
\begin{align}{2f(3)-5f(-2) = {32}} & \Rightarrow {2 \times 3a-(5 \times -2a) = {32}} \\
& \Rightarrow {6a-(-10a) = {32}} \\
& \Rightarrow {16a = 32} \\
& \Rightarrow {a = {32\over16}} \\
& \Rightarrow \color{fuchsia}{a = 2}
\end{align}

Donc la fonction linéaire cherchée est \({f(x) = 2x}\)


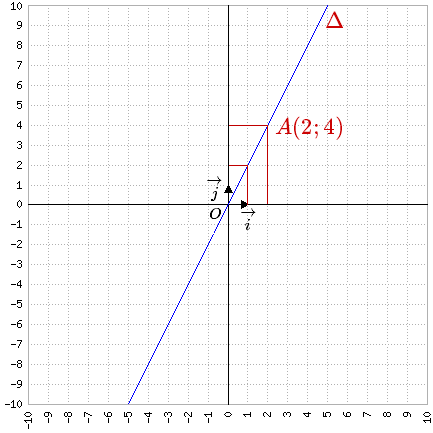
b) \({f}\) est une fonction linéaire donc sa représentation graphique est une droite \(\Delta\) passant par l'origine et par un point \(A(x,f(x))\).

Si \(x = 1\) donc \(f(x) = 1\times2 = \color{fuchsia}{2}\) ce qui nous donne \(\color{fuchsia}{A(1;2)}\)
Si \(x = 2\) donc \(f(x) = 2\times2 = \color{fuchsia}{4}\) ce qui nous donne \(\color{fuchsia}{A(2;4)}\).

ect...

Traçons la droite \(\Delta\)

Retour vers: Exercice corrigé n°07

Cours - Fonctions linéaires

Retour vers: Fonctions linéaires - Exercices corrigés - 1ère année secondaire