Correction - Exercice 09 page 66 - Vecteurs et translations
Vecteurs et translations
Exercice 09 page 66
\(A\) et \(B\) sont deux points distincts.
Déterminons dans chaque cas l'ensemble des points \(M\) et le construire.
1- \(\vec{AM}\) = \(\vec{AB}\)
\(\vec{AM}\) = \(\vec{AB}\) c'est à dire les deux points \(B\) et \(M\) sont confondus.
2- \(AM = AB\)
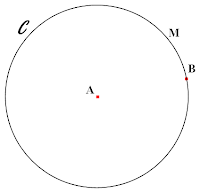
\(AM = AB\) c'est à dire l'ensemble des points \(M\) est le cercle \(C\) du centre \(A\) et de rayon \(AB\).
3- \(\vec{AM}\) = \(\vec{BM}\)
\(\vec{AM}\) = \(\vec{BM}\) \(\Rightarrow\)
\(\vec{AM}\) - \(\vec{BM}\)= \(\vec{0}\) \(\Rightarrow\)
\(\vec{AM}\) + \(\vec{MB}\)= \(\vec{0}\) \(\Rightarrow\)
\(\vec{AB}\)= \(\vec{0}\) ce qui veut dire que \(A\) et \(B\) sont deux points confondus, or \(A\) et \(B\) sont deux points distincts. Donc c'est impossible de trouver \(M\).
4- \(AM = BM\)
\(AM = BM\) signifie que l'ensemble des poins \(M\) est la médiatrice du segment \([AB]\).
5- \((AM) \perp (AB)\)
\(AM \perp AB\) signifie que l'ensemble des poins \(M\) est la droite perpendiculaire à \((AB)\) passant par le point \(A\).
6- \((AM) \perp (MB)\)
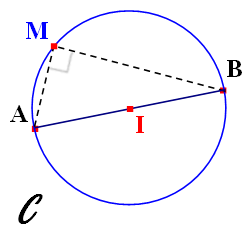
\((AM) \perp (MB)\) signifie que l'ensemble des poins \(M\) est le cercle \(C\) du centre \(I\) le milieu de \([AB]\), et de rayon \(IA\).
Déterminons dans chaque cas l'ensemble des points \(M\) et le construire.
1- \(\vec{AM}\) = \(\vec{AB}\)
\(\vec{AM}\) = \(\vec{AB}\) c'est à dire les deux points \(B\) et \(M\) sont confondus.
2- \(AM = AB\)
\(AM = AB\) c'est à dire l'ensemble des points \(M\) est le cercle \(C\) du centre \(A\) et de rayon \(AB\).
3- \(\vec{AM}\) = \(\vec{BM}\)
\(\vec{AM}\) = \(\vec{BM}\) \(\Rightarrow\)
\(\vec{AM}\) - \(\vec{BM}\)= \(\vec{0}\) \(\Rightarrow\)
\(\vec{AM}\) + \(\vec{MB}\)= \(\vec{0}\) \(\Rightarrow\)
\(\vec{AB}\)= \(\vec{0}\) ce qui veut dire que \(A\) et \(B\) sont deux points confondus, or \(A\) et \(B\) sont deux points distincts. Donc c'est impossible de trouver \(M\).
4- \(AM = BM\)
\(AM = BM\) signifie que l'ensemble des poins \(M\) est la médiatrice du segment \([AB]\).
5- \((AM) \perp (AB)\)
\(AM \perp AB\) signifie que l'ensemble des poins \(M\) est la droite perpendiculaire à \((AB)\) passant par le point \(A\).
6- \((AM) \perp (MB)\)
\((AM) \perp (MB)\) signifie que l'ensemble des poins \(M\) est le cercle \(C\) du centre \(I\) le milieu de \([AB]\), et de rayon \(IA\).
Libellés:
1ère année secondaire
Correction
Corrigées
exercice
Le Mathématicien
manuel scolaire
Math
Mathématiques
Vecteurs et translations






Aucun commentaire: