Correction - Exercice 03 page 78 - Somme de deux vecteurs - Vecteurs colinéaires
1ère année secondaire
Somme de deux vecteurs - Vecteurs colinéaires
Exercice 03 page 78
Traçons un triangle \(ABC\).
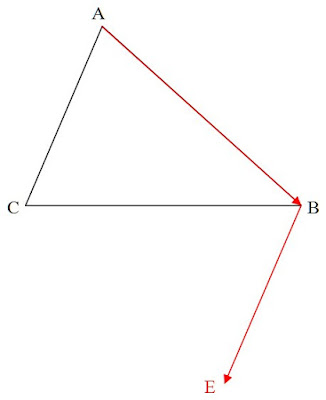
1- Plaçons le point \(E\) tel que \(\vec{AB}+\vec{AC}=\vec{AE}\).
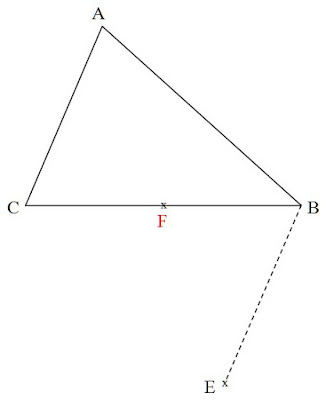
2- a) Plaçons le point \(F\) tel que \(\vec{BF}=\vec{FC}\).
\(\vec{BF}=\vec{FC}\) signifie \(F\) est le milieu de \([BC]\)
b) Montrons que \(F\) est le milieu de \([AE]\).
On a \(\vec{AE}=\vec{AB}+\vec{AC}\) donc \(ABCD\) est un parallélogramme et par la suite ([BC]\) et ([AE]\) ont le même milieu.
1- Plaçons le point \(E\) tel que \(\vec{AB}+\vec{AC}=\vec{AE}\).
2- a) Plaçons le point \(F\) tel que \(\vec{BF}=\vec{FC}\).
\(\vec{BF}=\vec{FC}\) signifie \(F\) est le milieu de \([BC]\)
b) Montrons que \(F\) est le milieu de \([AE]\).
On a \(\vec{AE}=\vec{AB}+\vec{AC}\) donc \(ABCD\) est un parallélogramme et par la suite ([BC]\) et ([AE]\) ont le même milieu.
Libellés:
1ère année secondaire
Correction
Corrigées
exercice
Le Mathématicien
manuel scolaire
Math
Mathématiques
Somme de deux vecteurs
Vecteurs colinéaires
Ex 1 page 223
RépondreSupprimer