Correction - Exercice 01 page 19 - Angles

1ère année secondaire

Angles

Exercice 01 page 19

Calculons les angles désignés par une lettre.

* Cherchons l'angle $a$ :
On a :

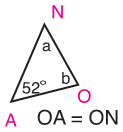
$OA=ON$ alors le triangle $OAN$ est isocèle en $I$.

$OAN$ est un triangle isocèle en $I$ signifie que l'angle $\widehat{O A N}=\widehat{A N O}=52°$.

Et par la suite :

$a=\widehat{A N O}=52°$.

Cherchons l'angle $b$ :
On a :
la somme des angles d'un triangle est égale à $180°$.

Donc :
$b=180°-(\widehat{A N O}+a)$$\Rightarrow$
$b=180°-(52°+52°)$$\Rightarrow$
$b=180°-104°$$\Rightarrow$
$b=76°$.

Conclusion :
$a=52°$ ; $b=76°$.

--------------------------------------------

* Cherchons l'angle $c$ :
On a :

$IT=IS$ alors le triangle $ITS$ est isocèle en $I$.

$OAN$ est un triangle isocèle en $I$ signifie que l'angle $\widehat{I T S}=\widehat{I S T}=c$.

Et puisque la somme des angles d'un triangle est égale à $180°$.

Donc :
$\widehat{T I S}+2c=180°$$\Rightarrow$
$90°+2c=180°$$\Rightarrow$
$2c=180°-90°$$\Rightarrow$
$2c=90°$$\Rightarrow$
$c=$$\frac{90}{2}$$\Rightarrow$
$c=$$45°$.

Conclusion :
$c=$$45°$.

--------------------------------------------

* Cherchons l'angle $\widehat{D U K}$ :
On a :
$DK=DU$ alors le triangle $DUK$ est isocèle en $D$.

$DUK$ est un triangle isocèle en $D$ signifie que l'angle $\widehat{D K U}=\widehat{D U K}=30°$.

Cherchons l'angle $\widehat{U D K}$ :
On a :
la somme des angles d'un triangle est égale à $180°$.

Donc :

$\widehat{U D K}=180°-(\widehat{D K U}+\widehat{U D K})$$\Rightarrow$

$\widehat{U D K}=180°-(30°+30°)$$\Rightarrow$
$\widehat{U D K}=180°-60°$$\Rightarrow$
$\widehat{U D K}=120°$.

Cherchons l'angle $f$ :
On a :
$\widehat{G D K}=180°$.

Donc :
$f=180°-\widehat{D K U}$$\Rightarrow$
$f=180°-120$$\Rightarrow$
$f=60°$.

Cherchons l'angle $g$ :
On a :
la somme des angles d'un triangle est égale à $180°$.

Donc :
$g=180°-(\widehat{D G U}+f)$$\Rightarrow$
$g=180°-(90°+60°)$$\Rightarrow$
$g=180°-150°$$\Rightarrow$
$g=30°$.

Conclusion :
$g=30°$ ; $f=60°$.

--------------------------------------------

Les droites de même couleur sont parallèles.

* Cherchons l'angle $m$ :

$m=180°-60°$$\Rightarrow$

$m=120°$.

Cherchons l'angle $i$ :

$i=60°$ (Si deux droites parallèles sont coupées par une sécante alors les angles alternes-internes sont deux à deux égaux).

Cherchons l'angle $k$ :

$k=i=60°$ (Si deux droites parallèles sont coupées par une sécante alors les angles correspondants sont deux à deux égaux).

Cherchons l'angle $j$ :

$j=180°-(k+(180°-130°))$$\Rightarrow$
$j=180°-(60°+50°)$$\Rightarrow$
$j=180°-110°$$\Rightarrow$
$j=70°$.

Conclusion :

$m=120°$ ; $i=60°$ ; $k=60°$ ; $j=70°$.

--------------------------------------------

* Cherchons l'angle $h$ :
On a :

la somme des angles d'un triangle est égale à $180°$.

Donc :

$2h+6h+h=180°)$$\Rightarrow$

$9h=180°$$\Rightarrow$

$h=$$\frac{180}{9}$$\Rightarrow$

$h=20°$.

Conclusion :

$h=20°$.

Retour vers: Exercice 01 page 19

Cours - Angles

Retour vers: Angles - Corrigées des exercices du manuel scolaire - 1ère année secondaire