Correction - S'auto-évaluer Vrai ou Faux page 191 - Fonctions linéaires

1ère année secondaire

Fonctions linéaires

S'auto-évaluer Vrai ou Faux page 191

1- Si l'image de \(1\) par une fonction linéaire est \(3\) alors le coefficient de cette fonction est égal à \(\frac{1}{3}\). Faux.

L'image de \(1\) égale à \(3\) signifie \(f(1)=3\) et puisque la fonction est linéaire alors \(f(1)=3\) équivaut à \(a\times1=3\) avec \(a\) le coefficient de cette fonction, et par la suite \(a\times1=3\) signifie \(a=\frac{3}{1}=3\).

Conclusion : la réponse est : Faux.

2- Si l'image de \(10\) par une fonction linéaire est \(8\) alors l'image de \(100\) est \(80\). Vrai.

L'image de \(10\) égale à \(8\) signifie \(f(10)=8\) et puisque la fonction est linéaire alors \(f(10)=8\) équivaut à \(a\times10=8\) avec \(a\) le coefficient de cette fonction, et par la suite \(a\times10=8\) signifie \(a=\frac{8}{10}=\frac{4}{5}\). donc la fonction \(f(x)=\frac{4}{5}x\).

Trouvons maintenant l'image de \(100\) par cette fonction :

\(f(100)=\frac{4}{5}\times100=\frac{400}{5}=80\).

Conclusion : la réponse est : Vrai.

3- Dans un repère \((O, I, J)\), les points \(O\), \(A (1, -5)\) et \(B (2,-9)\) sont alignés. Faux.

Par représentation graphique :

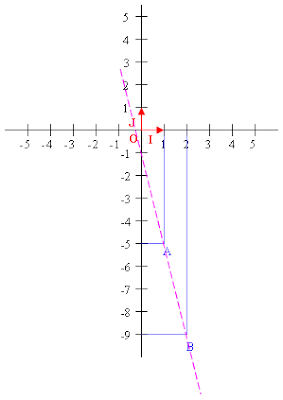
On représentant les points \(A\) et \(B\) dans un repère \((O, I, J)\) on constate que les points \(O\), \(A\) et \(B\) ne sont pas alignés.

Par calcul :

Cherchons l'équation de la droite \(\Lambda\) passant par \(O\) et \(A\) :
L'image de \(1\) égale à \(-5\) signifie \(f(1)=-5\) et puisque la fonction est linéaire alors \(f(1)=-5\) équivaut à \(a\times1=-5\) avec \(a\) le coefficient de cette fonction, et par la suite \(a\times1=-5\) signifie \(a=\frac{1}{-5}\). donc la fonction \(f(x)=-\frac{1}{5}x\), c'est à dire \(\Lambda\) a pour équation \(y=-\frac{1}{5}x\).

Cherchons l'équation de la droite \(\Lambda'\) passant par \(O\) et \(B\) :
L'image de \(2\) égale à \(-9\) signifie \(g(2)=-9\) et puisque la fonction est linéaire alors \(g(2)=-9\) équivaut à \(a\times2=-9\) avec \(a\) le coefficient de cette fonction, et par la suite \(a\times2=-9\) signifie \(a=\frac{2}{-9}\). donc la fonction \(g(x)=-\frac{2}{9}x\), c'est à dire \(\Lambda'\) a pour équation \(y=-\frac{2}{9}x\).

\(\Lambda:y=-\frac{1}{5}x\)

\(\Lambda':y=-\frac{2}{9}x\)


Donc \(\delta\) et \(\delta'\) sont deux droite sécante en \(O\) et par la suite \(O\), \(A\) et \(B\) ne sont pas parallèle.

Conclusion : la réponse est : Faux.

4- Diminuer un prix de \(25\%\) revient à le multiplier par \(0,75\). Vrai.

Diminuer un prix de \(25\%\) revient à le multiplier par \(1-\frac{25}{100}\) signifie \(\frac{100}{100}-\frac{25}{100}\) signifie \(\frac{75}{100}\) signifie \(0,75\).

Conclusion : la réponse est : Vrai.


5- Dans le graphique ci-contre, la droite \(D\) a pour équation \(y=\frac{3}{2}x\). Faux.

D'après le graphique on constate que l'image de \(3\) par une fonction linéaire est \(2\), et l'image de \(1\) égale à \(3\) signifie \(f(1)=3\) et puisque la fonction est linéaire alors \(f(1)=3\) équivaut à \(a\times1=3\) avec \(a\) le coefficient de cette fonction, et par la suite \(a\times1=3\) signifie \(a=\frac{1}{3}\). donc la fonction \(f(x)=\frac{1}{3}x\), c'est à dire \(D\) a pour équation \(y=\frac{1}{3}x\).

Conclusion : la réponse est : Faux.

Retour vers: S'auto-évaluer Vrai ou Faux page 191

Cours - Fonctions linéaires

Retour vers: Fonctions linéaires - Corrigées des exercices du manuel scolaire - 1ère année secondaire