Correction - S'auto-évaluer Recopier et compléter page 77 - Somme de deux vecteurs - Vecteurs colinéaires

1ère année secondaire 

Somme de deux vecteurs - Vecteurs colinéaires 

S'auto-évaluer Recopier et compléter page 77

Répondons par vrai ou faux

1- \(ABCD\) et \(AEFD\) sont deux parallélogrammes.

\(\vec{DA} + \vec{DC} = \vec{DB}\)

\(\vec{BC} + \vec{DC} = \vec{AC}\)

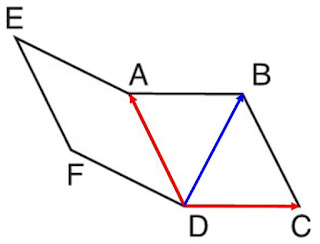
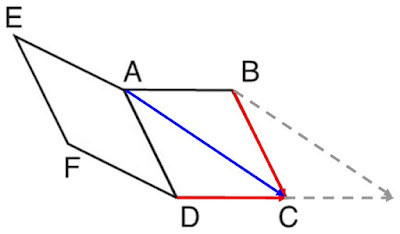
\(\vec{AB} + \vec{EF} = \vec{AC}\)

2- \(\vec{OA}= -\frac{3}{5}\vec{OC}\)

3- Si \(EF\) et \(GH\) sont deux vecteurs colinéaires et de même sens et \(GH = \frac{1}{2}EF\) alors \(\vec{EF} = 2\vec{GH}\).

4- Si \(\vec{AI}\) et \(\vec{ST}\) sont deux vecteurs colinéaires et de sens contraires et \(AI=3ST\) alors \(\vec{AI} = -3\vec{ST}\). (sens contraires)

5- Si \((AB)\) et \((CD)\) sont deux droites parallèles et \(M\) est un point de la droite \((AB)\) alors les vecteurs \(\vec{BM}\) et \(\vec{CD}\) sont colinéaires et de sens contraires.

Retour vers: S'auto-évaluer Recopier et compléter page 77

Cours - Somme de deux vecteurs - Vecteurs colinéaires

Retour vers: Somme de deux vecteurs - Vecteurs colinéaires - Corrigées des exercices du manuel scolaire - 1ère année secondaire