Correction - Exercice 08 page 78 - Somme de deux vecteurs - Vecteurs colinéaires

1ère année secondaire 

Somme de deux vecteurs - Vecteurs colinéaires 

Exercice 08 page 78

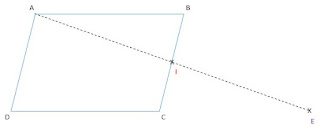
Soit ABCD un parallélogramme et $I$ le milieu de $[BC]$. 

Soit $E$ le symétrique de $A$ par rapport à $I$

Déterminons le réel $k$ vérifiant $\vec{DE}=k\vec{BA}$:

Puisque $E$ est le symétrique de $A$ par rapport à $I$, alors le quadrilatère $ABEC$ est un parallélogramme, et par la suite $\vec{EC}=\vec{BA}=\vec{CD}$.

On a aussi: $\vec{DE}=\vec{DC}+\vec{CE}$

Ce qui signifie: $\vec{DE}=-\vec{CD}+(-\vec{EC})$

Et puisque: $\vec{EC}=\vec{BA}=\vec{CD}$

Alors: $\vec{DE}=-\vec{BA}+(-\vec{BA})=-\vec{BA}-\vec{BA}$

D'où $\vec{DE}=-2\vec{BA}$ avec $k=-2$.

Retour vers: Exercice 08 page 78

Cours - Somme de deux vecteurs - Vecteurs colinéaires

Retour vers: Somme de deux vecteurs - Vecteurs colinéaires - Corrigées des exercices du manuel scolaire - 1ère année secondaire