Correction - Exercice 07 page 78 - Somme de deux vecteurs - Vecteurs colinéaires

1ère année secondaire 

Somme de deux vecteurs - Vecteurs colinéaires 

Exercice 07 page 78

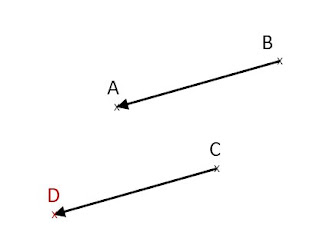
Soit \(A\), \(B\) et \(C\) trois points non alignés.

1- Construire le point \(D\) image de \(C\) par la translation de vecteur \(\vec{BA}\):

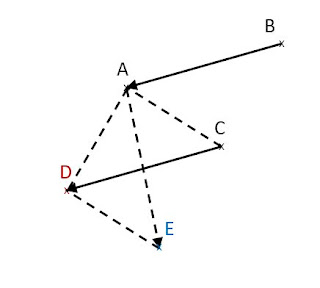
2- Construire le point \(E\) tel que \(\vec{AD}+\vec{AC}=\vec{AE}\):

3- Simplifions le vecteur \(\vec{AC}+\vec{DA}\)

\(\vec{AC}+\vec{DA}=\vec{DA}+\vec{AC}=\vec{DC}\)

4- Montrons que \(C\) est le milieu de \([BE]\)

on a: \(D=t_{\vec{BA}}(C)\) 

signifie que \(\vec{CD}=\vec{BA}\) et \(\vec{AD}=\vec{BC}\) et \(\vec{AD}+\vec{AC}=\vec{AE}\).

signifie que \(\vec{AD}=\vec{CE}\)

D'oû \(\vec{BC}=\vec{CE}\)

Donc \(C\) et \([BE]\) .

Retour vers: Exercice 07 page 78

Cours - Somme de deux vecteurs - Vecteurs colinéaires

Retour vers: Somme de deux vecteurs - Vecteurs colinéaires - Corrigées des exercices du manuel scolaire - 1ère année secondaire