Correction - Exercice 18 page 48 - Rapports trigonométriques d'un angle aigu - Relations métriques dans un triangle rectangle

1ère année secondaire

Rapports trigonométriques d'un angle aigu

Relations métriques dans un triangle rectangle

Exercice 18 page 48

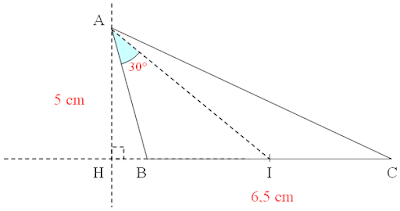
Soit \(ABC\) un triangle tel que \(I\) est le milieu de \([BC]\), \(AB=5\), \(BC=6,5\) et \(BAI=30°\).

a) Montrons que l'aire du triangle \(ABC\) est le double de l'aire du triangle \(ABI\) :

Soit \(S_1\) l'aire du triangle \(ABI\) et \(S_2\) l'aire du triangle \(ABC\).

Soit \(AH\) l'auteur du triangle \(ABI\) passant par \(A\) sur \((BI)\).

On sait que \(S_1=\frac{AH\times BI}{2}\)


Et puisque \(BI=\frac{BC}{2}\).

Alors \(S_1=\frac{AH\times \frac{BC}{2}}{2}\).

D'où \(S_1=\frac{\frac{AH \times BC}{2}}{2}\).

Et puisque \(S_2=\frac{AH\times BC}{2}\).

Alors \(S_1=\frac{S_2}{2}\).

Donc \(S_2=S_1\times 2\).


b) Calculons l'aire de \(ABC\) :

Soit \(H'\) la hauteur du triangle \(ABI\) passant par \(B\).

On a \(sin~30°=\frac{BH'}{AB}\).

D'où \(BH'=AB\times sin~30°=5 \times \frac{1}{2}=2,5cm\).

Cherchons \(AH'\) :
D'après le théorème de Pythagore dans le triangle rectangle \(H'BA\), \(AB^2=AH'^2+BH'^2\), alors \(AH'^2=AB'^2-BH'^2\) d'où \(AH'=\sqrt{AB'^2-BH'^2}=\sqrt{5^2-{2,5}^2}=\sqrt{18,75}=4,33cm\).

Cherchons \(IH'\) :
D'après le théorème de Pythagore dans le triangle rectangle \(H'BI\), \(BI^2=BH'^2+IH'^2\), alors \(IH'^2=BI^2-BH'^2\) d'où \(IH'=\sqrt{BI'^2-BH'^2}=\sqrt{{3,25}^2-{2,5}^2}=\sqrt{4,31}=2,08cm\).

Cherchons \(AI\) :
On a \(AI=AH'+H'I=4,33+2,08=6,41cm\).

Calculons l'aire de \(ABI\) :
\(S_1=\frac{BH'\times AI}{2}=\frac{2,5\times 6,41}{2}=8,01cm^2\).

Calculons l'aire de \(ABC\) :
On a \(S_2= 2\times S_1=2\times 8,01=16,02cm^2\).

Retour vers: Exercice 18 page 48

Cours - Rapports trigonométriques d'un angle aigu - Relations métriques dans un triangle rectangle - 1ère année secondaire

Retour vers: Rapports trigonométriques d'un angle aigu - Relations métriques dans un triangle rectangle - Corrigées des exercices du manuel scolaire - 1ère année secondaire