Correction - Exercice 14 page 193 - Fonctions linéaires
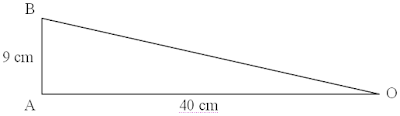
Soit le triangle \(OAB\) rectangle en \(A\), tels que \(OA=40\) et \(AB=9\).
Soit \(C\) un point de la demi-droite \([OA)\) et \(x=OC\).
La parallèle à \((AB)\) passant par \(C\) coupe \((OB)\) en un point D. On pose \(CD=y\) et \(OD=z\).
1- Trouvons \(OB\) :
D'après Pythagore \(OB^2=OA^2+AB^2=40^2+9^2=1600+81=1681\) d'où \(OB=\sqrt{1681}=41\).
2-
a) Donnons l'expression de \(y\) en fonction de \(x\) :
D'après Thalès \(\frac{OA}{OC}=\frac{AB}{DC}\) alors \(\frac{40}{x}=\frac{9}{y}\) d'où \(40y=9x\) donc \(y=\frac{9}{40}x\).
b) Donnons de deux manières, l'expression de \(z\) en fonction de \(x\) :
1) D'après Thalès \(\frac{OB}{OD}=\frac{OA}{OC}\) alors \(\frac{41}{z}=\frac{40}{x}\) d'où \(41x=40z\) donc \(z=\frac{41}{40}x\).
2) D'après Pythagore \(OD^2=OC^2+CD^2\) d'où \(z^2=x^2+y^2\) alors \(z^2=x^2+(\frac{9}{40}x)^2=x^2+(\frac{9}{40})^2.x^2=\frac{1600}{1600}x^2+\frac{81}{1600}x^2=\frac{1681}{1600}x^2\) d'où \(z=\frac{\sqrt{1681}}{\sqrt{1600}}x=\frac{41}{40}x\).
3- On note \(a\) l'aire du triangle \(OCD\).
a) Déterminons \(a\) lorsque \(x=1\)
Lorsque \(x=1\), \(y=\frac{9}{40}\times 1=\frac{9}{40}cm\).
D'où \(a=\frac{x\times y}{2}=\frac{1\times\frac{9}{40}}{2}=\frac{9}{40}\times\frac{1}{2}=\frac{9}{80}cm2\).
Déterminons \(a\) lorsque \(x=2\) :
Lorsque \(x=2\), \(y=\frac{9}{40}\times 2=\frac{9}{20}cm\).
D'où \(a=\frac{x\times y}{2}=\frac{2\times\frac{9}{20}}{2}=\frac{9}{20}cm2\).
b) Cherchons si l'aire \(a\) est une fonction linéaire de \(x\) :
Soit \(f\) la fonction tel que \(f(1)=\frac{9}{80}\) d'où son coefficient directeur est égale à \(\frac{\frac{9}{80}}{1}=\frac{9}{80}\), et par la suite \(f(x)=\frac{9}{80}x\).
Soit \(f'\) la fonction tel que \(f'(2)=\frac{9}{20}\) d'où son coefficient directeur est égale à \(\frac{\frac{9}{20}}{2}=\frac{9}{20}\times\frac{1}{2}=\frac{9}{40}\), et par la suite \(f'(x)=\frac{9}{40}x\)
Donc l'aire \(a\) n'est pas une fonction linéaire de \(x\) puisque le coefficient directeur de l'aire \(a\) en fonction de \(x\) n'est pas le même pour \(x=1\) et \(x=2\). Ou car \(f(x)\) est diffèrent de \(f'(x)\).
c) Déterminons \(a\) en fonction de \(x\) :
\(a\) est l'aire du triangle \(OCD\) donc \(a=\frac{OC\times CD}{2}=\frac{x\times y}{2}=\frac{x\times \frac{9}{40}x}{2}=\frac{\frac{9}{40}x^2}{2}=\frac{9}{40}x^2\times\frac{1}{2}=\frac{9}{80}x^2\)
Soit \(C\) un point de la demi-droite \([OA)\) et \(x=OC\).
1- Trouvons \(OB\) :
D'après Pythagore \(OB^2=OA^2+AB^2=40^2+9^2=1600+81=1681\) d'où \(OB=\sqrt{1681}=41\).
2-
a) Donnons l'expression de \(y\) en fonction de \(x\) :
D'après Thalès \(\frac{OA}{OC}=\frac{AB}{DC}\) alors \(\frac{40}{x}=\frac{9}{y}\) d'où \(40y=9x\) donc \(y=\frac{9}{40}x\).
b) Donnons de deux manières, l'expression de \(z\) en fonction de \(x\) :
1) D'après Thalès \(\frac{OB}{OD}=\frac{OA}{OC}\) alors \(\frac{41}{z}=\frac{40}{x}\) d'où \(41x=40z\) donc \(z=\frac{41}{40}x\).
2) D'après Pythagore \(OD^2=OC^2+CD^2\) d'où \(z^2=x^2+y^2\) alors \(z^2=x^2+(\frac{9}{40}x)^2=x^2+(\frac{9}{40})^2.x^2=\frac{1600}{1600}x^2+\frac{81}{1600}x^2=\frac{1681}{1600}x^2\) d'où \(z=\frac{\sqrt{1681}}{\sqrt{1600}}x=\frac{41}{40}x\).
3- On note \(a\) l'aire du triangle \(OCD\).
a) Déterminons \(a\) lorsque \(x=1\)
Lorsque \(x=1\), \(y=\frac{9}{40}\times 1=\frac{9}{40}cm\).
D'où \(a=\frac{x\times y}{2}=\frac{1\times\frac{9}{40}}{2}=\frac{9}{40}\times\frac{1}{2}=\frac{9}{80}cm2\).
Déterminons \(a\) lorsque \(x=2\) :
Lorsque \(x=2\), \(y=\frac{9}{40}\times 2=\frac{9}{20}cm\).
D'où \(a=\frac{x\times y}{2}=\frac{2\times\frac{9}{20}}{2}=\frac{9}{20}cm2\).
b) Cherchons si l'aire \(a\) est une fonction linéaire de \(x\) :
Soit \(f\) la fonction tel que \(f(1)=\frac{9}{80}\) d'où son coefficient directeur est égale à \(\frac{\frac{9}{80}}{1}=\frac{9}{80}\), et par la suite \(f(x)=\frac{9}{80}x\).
Soit \(f'\) la fonction tel que \(f'(2)=\frac{9}{20}\) d'où son coefficient directeur est égale à \(\frac{\frac{9}{20}}{2}=\frac{9}{20}\times\frac{1}{2}=\frac{9}{40}\), et par la suite \(f'(x)=\frac{9}{40}x\)
Donc l'aire \(a\) n'est pas une fonction linéaire de \(x\) puisque le coefficient directeur de l'aire \(a\) en fonction de \(x\) n'est pas le même pour \(x=1\) et \(x=2\). Ou car \(f(x)\) est diffèrent de \(f'(x)\).
c) Déterminons \(a\) en fonction de \(x\) :
\(a\) est l'aire du triangle \(OCD\) donc \(a=\frac{OC\times CD}{2}=\frac{x\times y}{2}=\frac{x\times \frac{9}{40}x}{2}=\frac{\frac{9}{40}x^2}{2}=\frac{9}{40}x^2\times\frac{1}{2}=\frac{9}{80}x^2\)
Libellés:
1ère année secondaire
Correction
Corrigées
exercice
Fonctions linéaires
Le Mathématicien
manuel scolaire
Math
Mathématiques




Aucun commentaire: