Correction - Exercice 05 page 78 - Somme de deux vecteurs - Vecteurs colinéaires

1ère année secondaire 

Somme de deux vecteurs - Vecteurs colinéaires 

Exercice 05 page 78

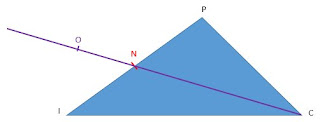
Soit $PIC$ un triangle.

1- Soit $N$ le milieu de $[PI]$ et $O$ un point de la droite $(CN)$.

1- Construire le point $R$ tel que $\vec{PR}=\vec{PI}+\vec{PC}$:

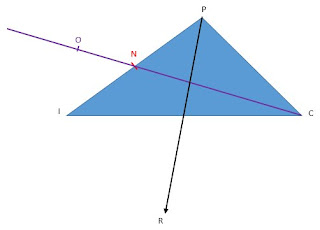
Construire le point $S$ tel que $\vec{PR}=\vec{PS}+\vec{PO}$:

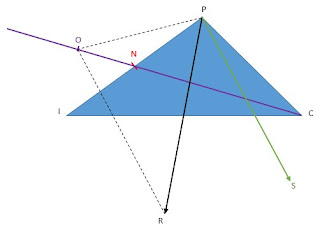
2- Montrons que $\vec{SI}=\vec{CO}$. En déduire que les droites $(SI)$ et $(CN)$ sont parallèles:

$\vec{PR}=\vec{PI}+\vec{PC}$ signifie $PIRC$ est un parallélogramme 

$\vec{PR}=\vec{Ps}+\vec{PO}$ signifie $PORS$ est un parallélogramme 

Alors  $[PR], [IC] et [OS]$ ont même milieu, donc $OCSI$ est un parallélogramme d'oû $\vec{SI}=\vec{CO}$.

Et puisque $\vec{CN}=\vec{CO}$ sont colinéaires alors les droites $SI$ et $CN$ sont paralléles.

Retour vers: Exercice 05 page 78

Cours - Somme de deux vecteurs - Vecteurs colinéaires

Retour vers: Somme de deux vecteurs - Vecteurs colinéaires - Corrigées des exercices du manuel scolaire - 1ère année secondaire