Correction - Exercice 10 page 47 - Rapports trigonométriques d'un angle aigu - Relations métriques dans un triangle rectangle

1ère année secondaire

Rapports trigonométriques d'un angle aigu

Relations métriques dans un triangle rectangle

Exercice 10 page 47

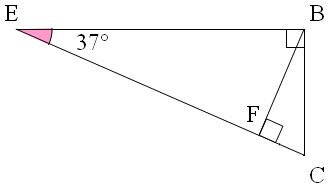
Soit un rectangle \(ABCD\) et les points \(E\) et \(F\) appartenant respectivement aux segments \([AB]\) et [EC], \(EB=ED=10cm\), \(\widehat{CEB}=37°\) et \(\widehat{BFE}=90°\).

1- Elaborons une stratégie de construction de cette figure.
D'abord on commence à construire \(EBC\) rectangle en \(B\) et tel que \(\widehat{BEC}=37°\) et le point \(F\) tel que \(\widehat{BFE}=90°\) :

Ensuite on trace la parallèle à \(EB\) passant par \(C\) sur laquelle on marque le point \(D\) tel que \(EB=ED\) :

En fin on marque le point \(A\) tel que \(ABCD\) soit un parallélogramme :

2- Calculons \(EF\), \(BC\) et \(sin~\widehat{AED}\).

On a : 

* \(cos~37°=\frac{EF}{EB}\) d'où \(EF=EB\times cos~37°=10\times 0,8=8 cm\).

* \(tan~37°=\frac{BC}{EB}\) d'où \(BC=EB\times tan~37°=10\times 0,75=7,5 cm\).

* \(\widehat{AED}=\frac{AD}{ED}=\frac{7,5}{10}=0,75\).

3- Donnons une valeur approchée à \(0,1\) près de l'aire du triangle \(DEC\).

Cherchons \(AE\) :
Le triangle \(DEC\) est rectangle en \(A\) et d'après Pythagore on a  \(ED^2=AD^2+AE^2\).
D'où \(AE^2=ED^2+AD^2=10^2+7,5^2=100-56,25=43.75\).
Donc : \(AE=\sqrt{43.75}=6,61cm\).


Cherchons l'aire \(A\) du triangle \(DEC\) :

\(A=\frac{DC\times EH}{2}\) et puisque \(DC=AB\) et \(EH=BC\) alors \(A=\frac{AB\times BC}{2}=\frac{(AE+EB)\times 7,5}{2}=\frac{(6,61+10)\times 7,5}{2}=\frac{16,61\times 7,5}{2}==62,2875=62.3cm^2\).

Retour vers: Exercice 10 page 47

Cours - Rapports trigonométriques d'un angle aigu - Relations métriques dans un triangle rectangle - 1ère année secondaire

Retour vers: Rapports trigonométriques d'un angle aigu - Relations métriques dans un triangle rectangle - Corrigées des exercices du manuel scolaire - 1ère année secondaire