Correction - Exercice 16 page 48 - Rapports trigonométriques d'un angle aigu - Relations métriques dans un triangle rectangle

1ère année secondaire

Rapports trigonométriques d'un angle aigu

Relations métriques dans un triangle rectangle

Exercice 16 page 48

Soit \(ABC\) un triangle, avec \(BC = a\), \(AB = c\), \(AC = b\), \(R\) le rayon de son cercle circonscrit et \(S\) la mesure de l'aire de \(ABC\).

On se propose d'établir la relation \(4RS = abc\).

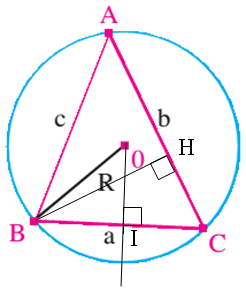
a) Traçons la hauteur \([BH]\) :

Exprimons \(BH\) en fonction de \(c\) et \(sin~\widehat{BA}\) :
Dans le triangle \(ABC\) on a \(sin~\widehat{A} = \frac{BH}{AB}=\frac{BH}{c}\) donc \(BH = c~sin~\widehat{A}\).

Exprimons \(S\) en fonction de \(b\), \(c\) et \(sin~\widehat{A}\) :
\(S\) est l'aire du triangle \(ABC\), c'est à dire \(S=\frac{AC \times BH}{2}=\frac{b \times BH}{2}=\frac{b \times c~sin~\widehat{A}}{2}\) puisque \(BH = c~sin~\widehat{A}\).

Déduisons une expression de \(sin~\widehat{A}\) :
D'après la solution prétendante trouvé on a :
\(S=\frac{b \times c~sin~\widehat{A}}{2}\)

D'où \(sin~\widehat{A}=\frac{2S}{bc}\)

b) Marquons \(I\) milieu de \([BC]\) :

Montrons que \(\widehat{BOI}=\widehat{A}\) :

Exprimons \(sin~\widehat{A}\) en fonction de \(a\) et \(R\) :

\(OBC\) est un triangle isocèle alors \(OI\) est la bissectrice de l'angle \(\widehat{BOC}\) d'où \(\widehat{BOI}=\frac{\widehat{BOC}}{2}\) et par la suite \(\widehat{BOI}=\widehat{A}\) et on en déduit que \(sin~\widehat{A}=sin~\widehat{BOI}=\frac{BI}{R}=\frac{\frac{a}{2}}{R}=\frac{a}{2R}\).

Conclusion : \(sin~\widehat{A}=\frac{a}{2R}\)

c) Déduisons de ce qui précède la relation \(4RS = abc\) :

On a trouvé que \(sin~\widehat{A}=\frac{2S}{bc}\) et \(sin~\widehat{A}=\frac{a}{2R}\) d'où \(\frac{2S}{bc}=\frac{a}{2R}\) donc \(2S \times 2R=abc\)

Conclusion : \(4RS=abc\)

Retour vers: Exercice 16 page 48

Cours - Rapports trigonométriques d'un angle aigu - Relations métriques dans un triangle rectangle - 1ère année secondaire

Retour vers: Rapports trigonométriques d'un angle aigu - Relations métriques dans un triangle rectangle - Corrigées des exercices du manuel scolaire - 1ère année secondaire