Correction - Exercice 06 page 208 - Equations et inéquations du premier degré à une inconnue

1ère année secondaire 

Equations et inéquations du premier degré à une inconnue 

Exercice 06 page 208 

Résolvons dans \(\mathbb{R}\) chacune des inéquations suivantes et donnons les solutions sous forme d'intervalles :

a) \(-3x+1≤0\).

\(-3x+1\leq0\) \(\Rightarrow\) \(-3x\leq-1\) \(\Rightarrow\) \(3x\geq1\) \(\Rightarrow\) \(x\geq\frac{1}{3}\).

D'où \(S_\mathbb{R}=[\frac{1}{2};+\infty[\).

b) \(-\frac{x}{4}≤\frac{1}{5}-\frac{x}{3}\).

\(-\frac{x}{4}\leq\frac{1}{5}-\frac{x}{3}\) \(\Rightarrow\) \(-\frac{x}{4}+\frac{x}{3}\leq\frac{1}{5}\) \(\Rightarrow\) \(-\frac{3x}{12}+\frac{4x}{12}\leq\frac{1}{5}\) \(\Rightarrow\) \(\frac{x}{12}\leq\frac{1}{5}\) \(\Rightarrow\) \(\frac{1}{12}x\leq\frac{1}{5}\) \(\Rightarrow\) \(x\leq\frac{\frac{1}{5}}{\frac{1}{12}}\) \(\Rightarrow\) \(x\leq\frac{1}{5}\times\frac{12}{1}\) \(\Rightarrow\) \(x\leq\frac{12}{5}\) \(\Rightarrow\)

D'où \(S_\mathbb{R}=]-\infty;\frac{12}{5}]\).

c) \(x(x+1)>x^2+3\).

\(x(x+1)>x^2+3\) \(\Rightarrow\) \(x^2+x>x^2+3\) \(\Rightarrow\) \(x^2-x^2+x>3\) \(\Rightarrow\) \(x>3\).

D'où \(S_\mathbb{R}=]3;+\infty[\).

d) \(5(2-x)-3(5x-1)≥\frac{3x}{4}\).

\(5(2-x)-3(5x-1)≥\frac{3x}{4}\) \(\Rightarrow\) \(10-5x-15x+3≥\frac{3x}{4}\) \(\Rightarrow\) \(-20x–\frac{3}{4}x≥-13\) \(\Rightarrow\) \(-\frac{80}{4}x-\frac{3}{4}x≥-13\) \(\Rightarrow\) \(-\frac{83}{4}x≥-13\) \(\Rightarrow\) \(\frac{83}{4}x\leq13\) \(\Rightarrow\) \(x\leq\frac{13}{\frac{83}{4}}\) \(\Rightarrow\) \(x\leq13\times\frac{4}{83}\) \(\Rightarrow\) \(x\leq\frac{52}{83}\).

D'où \(S_\mathbb{R}=]-\infty;\frac{52}{83}]\).

e) \(10^{-5}x+121<2.10^{-4}x–57\).

\(10^{-5}x+121<2.10^{-4}x-57\) \(\Rightarrow\) \(10^{-5}x-2.10^{-4}x<-57-121\) \(\Rightarrow\) \((10^{-5}-2.10^{-4})x<-178\) \(\Rightarrow\) \((\frac{1}{10^{5}}-\frac{2}{10^{4}})x<-178\) \(\Rightarrow\) \((0,00001-0,0002)x<-178\) \(\Rightarrow\) \(-0,00019x<-178\) \(\Rightarrow\) \(0,00019x>178\) \(\Rightarrow\) \(x>\frac{178}{0,00019}\).

D'où \(S_\mathbb{R}=]\frac{178}{0,00019};+\infty[\).

f) \(25(x+2)≥2(x–25)\).

\(25(x+2)≥2(x-25)\) \(\Rightarrow\) \(25x+50≥2x-50\) \(\Rightarrow\) \(25x-2x≥-50-50\) \(\Rightarrow\) \(23x≥-100\) \(\Rightarrow\) \(x≥-\frac{100}{23}\).

D'où \(S_\mathbb{R}=[-\frac{100}{23};+\infty[\).

g) \(4–[2x–(x+1)^2]=(x–4)(x–1)\).

Elle n'est pas une inéquation.

h) \(\frac{x-4}{2}–\frac{3-x}{4}≤2(x–1)+\frac{x-1}{3}\).

\(\frac{x-4}{2}-\frac{3-x}{4}≤2(x-1)+\frac{x-1}{3}\) \(\Rightarrow\) \(\frac{2\times(x-4)}{4}-\frac{3-x}{4}≤ \frac{3\times 2(x-1)}{3}+\frac{x-1}{3}\) \(\Rightarrow\) \(\frac{2x-8}{4}-\frac{3-x}{4}≤\frac{6x-6}{3}+\frac{x-1}{3}\) \(\Rightarrow\) \(\frac{2x-8-(3-x)}{4}≤\frac{6x-6+x-1}{3}\) \(\Rightarrow\) \(\frac{3x-11}{4}≤\frac{7x-7}{3}\) \(\Rightarrow\) \(3\times\frac{3x-11}{12}≤4\times\frac{7x-7}{12}\) \(\Rightarrow\) \(9x-33≤28x-28\) \(\Rightarrow\) \(9x-28x≤-8+33\) \(\Rightarrow\) \(-19x≤5\) \(\Rightarrow\) \(x\geq-\frac{5}{19}\).

D'où \(S_\mathbb{R}=[-\frac{5}{19};+\infty[\).

i) \(3x–(x–1)<\frac{1}{3}(6x+5)\).

\(3x-(x-1)<\frac{1}{3}(6x+5)\) \(\Rightarrow\) \(3x-x+1<\frac{6}{3}x+\frac{5}{3}\) \(\Rightarrow\) \(2x+1<2x+\frac{5}{3}\) \(\Rightarrow\) \(2x-2x<\frac{5}{3}-1\) \(\Rightarrow\) \(0x<\frac{5}{3}-\frac{3}{3}\) \(\Rightarrow\) \(0x<\frac{2}{3}\) donc pour tout \(x\in\mathbb{R}\) l'inéquation est vrai.

D'où \(S_\mathbb{R}=\mathbb{R}\).

j) \(2x+\frac{2x+3}{5}≥\frac{3}{4}(2x-1)-\frac{9}{2}\).

\(2x+\frac{2x+3}{5}≥\frac{3}{4}(2x-1)-\frac{9}{2}\) \(\Rightarrow\) \(\frac{10x}{5}+\frac{2x+3}{5}≥\frac{6}{4}x-\frac{3}{4}-\frac{9}{2}\) \(\Rightarrow\) \(\frac{12x}{5}+\frac{3}{5}≥\frac{6}{4}x-\frac{3}{4})-\frac{18}{4}\) \(\Rightarrow\) \(\frac{12x}{5}-\frac{6}{4}x≥-\frac{21}{4})-\frac{3}{5}\) \(\Rightarrow\) \(\frac{48x}{20}-\frac{30}{20}x≥-\frac{105}{20})-\frac{12}{20}\) \(\Rightarrow\) \(\frac{18x}{20}≥-\frac{117}{20}\) \(\Rightarrow\) \(18x≥-117\) \(\Rightarrow\) \(x\leq-\frac{117}{18}\) \(\Rightarrow\) \(x\leq-\frac{13}{2}\).

D'où \(S_\mathbb{R}=[-\infty;-\frac{13}{2}]\).

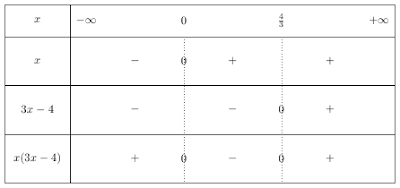
k) \(x(3x-4)<0\).

\(x(3x-4)<0\) est un produit, et pour résoudre cette inéquation on doit étudie le signe de chaque facteur. 

Les facteurs sont : \(x\) et \(3x-4\).

Le premier facteur s'annule lorsque \(x=0\) et le deuxième facteur s'annule lorsque \(x=\frac{4}{3}\).

\(x(3x-4)\) est strictement négatif donc on choisi l'intervalle ou il y a le signe \(-\).

D'où \(S_\mathbb{R}=]0;\frac{4}{3}[\).

l) \((4-x)(x-4)≤0\).

Les facteurs sont : \(4-x\) et \(x-4\).

Le deux facteurs s'annulent lorsque \(x=4\).

\((4-x)(x-4)\) est négatif donc on choisi l'intervalle ou il y a le signe \(-\). 

D'où \(S_\mathbb{R}=]-\infty;+\infty[=\mathbb{R}\).

m) \(x^2–5x≥0\).

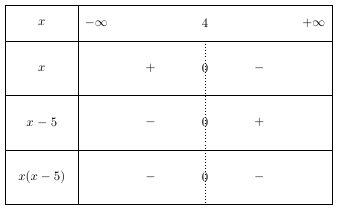
\(x^2-5x≥0\) \(\Rightarrow\) \(x(x-5)≥0\).

Les facteurs sont : \(x\) et \(x-5\).

Le premier facteur s'annule lorsque \(x=0\) et le deuxième facteur s'annule lorsque \(x=5\).

\(x(x-5)\) est positif donc on choisi l'intervalle ou il y a le signe \(+\). 

D'où \(S_\mathbb{R}=]-\infty;0]\cup[5;+\infty[\).

Retour vers: Exercice 06 page 208

Cours - Equations et inéquations du premier degré à une inconnue

Retour vers: Equations et inéquations du premier degré à une inconnue - Corrigées des exercices du manuel scolaire - 1ère année secondaire