Correction - Exercice 12 page 34 - Théorème de Thalès et sa réciproque

1ère année secondaire

Théorème de Thalès et sa réciproque

Exercice 12 page 34

1- On construit \((C1)\) le cercle de diamètre \([AB]\) et \((C2)\) le cercle de diamètre \([BC]\).

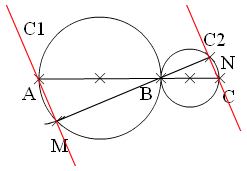
2- Soit \(M\) un point de \((C1)\) tel que \(AM =1,5cm\).
La droite \((BM)\) coupe \((C2)\) en \(N\).

a) Montrer que les droites \((AM)\) et \((NC)\) sont parallèles.

On a :

\(ABM\) un triangle rectangle en \(M\) et \(BCN\) un triangle rectangle en \(N\), et puisque \(AM\) et \(CN\) sont perpendiculaire à la même droite \(MN\) donc elles sont parallèles

b) Calculer \(CN\) et \(BN\).

D'après le théorème de Thalès on a :

\(\frac{BC}{BA}\) \(=\) \(\frac{CN}{AM}\)

D'où \(CN=\) \(\frac{BC\times AM}{BA}\) \(=\) \(\frac{2\times 1,5}{4}\) \(=\) \(\frac{3}{4}\)\(cm\).

D'après le théorème Pythagore dans le triangle \(BCN\) on a :

\(BN^2+CN^2=BC^2\) \(\Rightarrow\)

\(CN^2=BC^2-BN^2\) \(\Rightarrow\)

\(CN^2=2^2-{(\frac{3}{4})}^2\) \(\Rightarrow\)

\(CN^2=4-\frac{9}{16}\) \(\Rightarrow\)

\(CN^2=\frac{64}{16}-\frac{9}{16}\) \(\Rightarrow\)

\(CN^2=\frac{55}{16}\) \(\Rightarrow\)

\(CN=\sqrt{\frac{55}{16}}=\frac{1}{4}\sqrt{55}cm\).

Retour vers: Exercice 12 page 34

Cours - Théorème de Thalès et sa réciproque

Retour vers: Théorème de Thalès et sa réciproque - Corrigées des exercices du manuel scolaire - 1ère année secondaire